Theory of Physical Treatment of Water
prepared by Under Construction
Professor Young I. Cho, Ph.D., Department of Mechanical Engineering & Mechanics
Drexel University, Philadelphia, PA 19104
Web Site:
http://httpsrv.irt.drexel.edu/faculty/choyiIntroduction
Scale is formed in many water-processing applications such as boilers, heat exchangers, condensers, evaporators, cooling towers, and pipe walls. Scale often observed in industry includes calcium carbonate, calcium sulfate, barium sulfate, silica, iron scales, and others. The types of scale differ from industry to industry, depending on the contents of available water. One of the most common forms of scale is calcium carbonate (CaCO3), which occurs naturally as an ingredient of chalk, limestone, and marble. Water passing over and permeating through rocks dissolves calcium carbonate, and when this water subsequently flows through a water system the calcium carbonate precipitates out to form a hard scale. This clogs pipes and encrusts heat transfer surfaces. Usually the correction of the problem of scale build-up is accomplished by acid cleaning, scraping, and water or sand blasting, an operation which incurs downtime and repair costs.
Various chemicals are successfully used to prevent scale by reducing water hardness and silica as well as removing alkalinity. Acid cleaning has been effective in removing existing scale and is a part of routine maintenance. However, the cost of chemical treatment recurs every month in most cases. Furthermore, the loss of equipment material due to the acid cleaning is of a matter of concern.
This paper presents a theory of physical (i.e., non-chemical) water treatment representing an environmentally clean technology to prevent and remove scales. The physical water treatment offers an alternative to the chemical water treatment. History shows that there were attempts to treat water-using magnets two to three thousand years ago. In the United States, there have been numerous efforts for the past 150 years to introduce various physical water treatments as manifested by the long list of patents awarded by the U.S. patent office.
One of the major problems in the physical water treatment is the lack of understanding of its operating principle (or theory). Currently there are more than 100 companies marketing different types of physical water treatment products in the world. Each provides a paragraph explaining how its product works. Some of the claims are correct and acceptable while many are at fault from the perspective of fundamental physics and physical chemistry. Furthermore, most claims are testimonial statements. For example, they state that the treatment completely cleaned old scales from pipe in two months. Although these statements collected from field applications are very valuable and helpful in marketing, they do not add much in understanding the theory of the physical water treatment. The objective of this paper is to review the fundamental theory on which all physical water treatment products are based.
Background
Scale deposition mechanism is often explained by a process that includes dissolution of minerals, supersaturation, nucleation, precipitation, crystal growth, and, finally, scale deposition. Many variables control the scale deposition mechanism. The three most important variables are pH, temperature and pressure, because the solubility of scale-causing minerals are critically dependent on these three variables. The solubility of calcium carbonate decreases with increasing pH and temperature whereas it decreases with decreasing pressure. When conditions such as pH, temperature, and pressure change in a flow system such that the solubility of scale-causing minerals decreases, the electrostatic Coulombic attraction between the dissolved mineral ions and metal surfaces makes these minerals stick to the surfaces. This is why scales are unavoidable without some active scale prevention measures.
Many billions of dollars are lost due to the equipment failure or replacement caused by scale build-up. For example, most heat exchangers used in a hard water area need regular maintenance every three to six months and a major overhaul every three to five years. Thus, reduction or prevention of scale deposits would create huge economic benefits. In fact, if we successfully demonstrate the effectiveness of any physical water treatment technology in preventing and removing scales, then this technology will revolutionize many industries, including power, agricultural (i.e., poultry), mining, chemical, marine (i.e., ships), food processing, pharmaceutical industries to name a few.
The Confusion
It is well known that there are two types of calcium carbonates: calcite and aragonite as shown in Fig. 1. In all chemistry textbooks and relevant reference books, calcite is described consistently as the calcium carbonate which is formed at a lower temperature (i.e., below 30oC), easily removable with weak acid, less-adherent than aragonite, having a hexagonal crystal shape and a specific gravity of 2.71. Aragonite is described as the one which is formed at high temperature (i.e., above 30oC), difficult to remove, having an orthorhombic crystal shape and a specific gravity of 2.94. Specifically, they describe the aragonite as a more dangerous form of calcium carbonate in boiler and other heat transfer equipment since it forms a harder and denser deposit than the calcite. When calcium carbonate is formed at temperature above 30oC, both aragonite (~80%) and calcite (~20%) are formed. However, at a temperature below 30oC, almost all the calcium carbonates are calcite. This is one of the important facts which should be clarified in order to propose the present theory of water treatment in this paper. The confusion was caused by the physical water treatment industry in their commercial brochures, where calcite was described as the more dense and more-adherent than aragonite. It is time to correct the mistake.
Classification of Water Treatment Methods
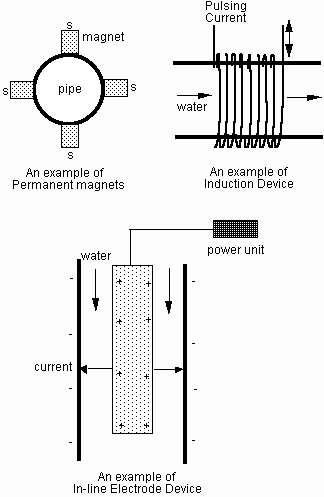
Most water treatment devices can be classified in three categories: permanent magnets, induction device, and in-line electrodes. Figure 2 shows a typical example of each device. Note that the actual arrangements in commercial devices can be quite different from the illustrations in Fig. 2. Devices using permanent magnets critically depend on the magnetic strength of permanent magnet, and the average strength of permanent magnet is in the range of 4,000 to 6,000 gauss as shown in the table below.
Induction devices utilize complex pulsing current to produce induced oscillating electric field inside pipes. In most cases, the magnetic field produced from the induction is slightly larger than the earth's magnetic field so the induction device should not be considered as a magnetic device at all.
Type of magnets Strength (Gauss)
____________________________________________________
Induction device 0.1 - 10
refrigerator magnets that hold notes 100
bar magnet 100 - 1,000
scale removing magnets 4,000 - 6,000
large scientific magnets 20,000 - 40,000
superconducting magnets 5,000,000 - 10,000,000
_____________________________________________________
Table: Comparison of magnetic strength

Fig. 2 Examples of permanent magnet, induction device, and in-line electrode device
Devices based on in-line electrodes use a high energy electrode at the center of pipe and also utilize complex pulsing currents between the center electrode and wall, where water makes direct contact with the center electrode and wall section. This in-line technology requires cutting of an existing pipe. Although cutting the existing pipe is a major challenge from the installation and marketing point of view, this in-line technology provides very effective means of treating water due to the direct contact between the in-line unit and water. The in-line technology uses one of the following: electromagnetic, electrostatic, electronic, or ultrasound methods. All four methods have positive effects on the interference of crystalline formation. The electrostatic unit requires a relatively high voltage whereas the electronic unit does not.
Review of Prior Theories
A brief review of a few of the prior theories and research is appropriate at this point. Moody [U.S. Patent 3,228,878] pointed out that scale-causing particles including calcium carbonate, magnesium carbonate, silicon dioxide are diamagnetic, i.e., repelled by the magnetic. He proposed a scale prevention method through an alteration of the energy content of the diamagnetic substances.
It has been claimed in commercial brochures of permanent magnets that when water is treated by a strong permanent magnet, the scale-causing ions (mostly diamagnetic) become magnetized instantaneously, having induced magnetic dipole. Consequently, these diamagnetic scale-causing ions repel each other, resulting in the prevention of scale build-up and removal of existing scales. The magnetization lasts over some distance and period even after the diamagnetic scale-causing ions leave the area under the strong magnetic field. To the best of our knowledge, these claims can not be justified by the laws of physics. A similar claim of a single, instantaneous jolt to break large clusters of scale-causing diamagnetic molecules has been made. The existence of the large clusters in a saturated or even in a supersaturated solution can not be justified based on thermodynamic principles. All scale-causing ions in solution are in a dissolved state, and the solution becomes supersaturated when parameters such as pH, temperature, pressure, etc. change, thus, resulting in the precipitation of diamagnetic clusters.
The induced magnetic moments or simply magnetization M of a material is defined as the net magnetic moment per unit volume, i.e., the vector sum of all the atomic magnetic moments in a unit volume. Conventionally, the ratio of the induced magnetization to the applied magnetic field, M/B, is called the magnetic susceptibility. In non-ferromagnetic materials, the induced magnetic forces are so much smaller than the electric forces, that thermal motions can knock out the alignment by the atomic dipole moments even at temperatures as low as a few tenths of a degree Kelvin. So, it would be impossible to have any permanent lining up of the magnets at room temperature [Feynman et al. Vol. II, p.34-2]. The above statement was made for solid. Thus, the permanent lining up of diamagnetic scale-causing ions in liquid is not possible. Therefore, the claim that the scale-causing ions become magnetized instantaneously, having induced magnetic dipole, is not correct.
Spiegel [1] proposed a mechanism in support of his patent which focuses on what he describes as the specific work function. This is the shift of electrons on the surface of a solid which he claims to accomplish through the use of a rotating disc of permanent magnets. This shift in electronic charge will affect the rate of growth and the morphology of the growing crystal. He cites the experimental work of Donaldson and Grimes [2], who found that untreated water would preferentially form aragonite, whereas magnetically treated water would preferentially form calcite.
Herzog et. al [3] focused on the effect of iron, which is generally present in natural waters, and is highly affected by magnetic fields. They have presented experimental evidence that in the presence of iron ions, the growth of calcite is inhibited, while aragonite growth is unaffected. Iron also inhibited the natural conversion of aragonite into calcite. It was suggested that magnetic treatment could possibly induce the liberation of iron into the water stream, thus inhibiting the growth of scale.
De Baat [4] has proposed in his patent that the magnetic treatment affects the orientation of the water molecule itself. This orientation is proposed to result in the ions of impurities (calcium and magnesium) coming out of solution. The resulting precipitate forms in the water as opposed to nucleating at the wall surface of the pipe. These loose precipitates can then be filtered out of solution.
Kronenberg [5] studied the effects of permanent magnets on water by preparing water samples dried on glass slides for microscopic observation. He found microscopic evidence indicating a change in crystal formation due to the magnetic treatment. Calcium carbonate in untreated water was found to crystallize in massive, prismatic crystals along the solid/water interface. Treated water formed circular crystals not at the interface but within the water phase. The circular crystals would re-crystallize slowly over a period of days and then dissolve back into solution. The proposed mechanism is based on the energy absorbed by the water molecules. He states that the internal frequency of the water ‘cage’ formed from hydration of particles in solution is in the range of 1-10 kHz, with a multiple-magnetic configuration able to supply this.
One of the common observations in the use of permanent magnets in water treatment is the effect of flow velocity on the effectiveness of water treatment device. Moody [U.S. Patent 3,228,878] mentioned that approximately one half foot per second was sufficient for most scale-causing substances. Kronenberg [5] reports that the relationship between the effectiveness of permanent magnets and flow velocity has in almost all cases a maximum for one velocity. In his tests, he reported the optimum velocity of 2.5 and 4.6 m/s for single and double distances between magnets, respectively. Bartz [private communication] reports that the threshold flow velocity in most cases was 23 ft/s (i.e., 7 m/s), above which permanent magnets work the best. Mag-Well reduces the cross-sectional area by approximately 75% in order to increase the flow velocity, where they install permanent magnets. In the use of permanent magnets, it appears that the flow velocity plays a major role, and the reason for that has not been clearly explained.
Past claims can be broadly categorized into two areas - magnetic or electric effects on (1) water and (2) crystal formation. The former can be briefly described below and the latter will be described in the subsequent sections. According to water chemistry most water molecules are locked in aggregates in liquid water, and less than 20% exist as free water molecules [cite Bailar]. This is because water molecules have a dipole moment - the hydrogen atom is attracted to the oxygen atom of the adjacent water molecule. Most physical water treatment devices produce molecular agitation whose frequency is tuned to the natural frequency of the water molecules vibrating in the aggregates. Through the cooperative resonance of the water molecules, free water molecules become available, dissolving existing scales. Figure 3 shows a schematic diagram of the above-mentioned resonance process to break the hydrogen bonds in water aggregates.
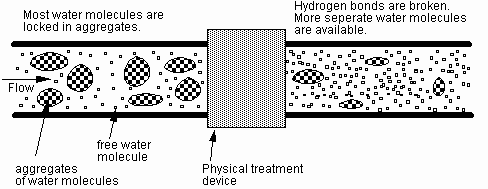
Fig. 3 Schematic diagram of proposed hypothesis: liquid water clusters are broken into free separate water molecules.
Although there are substantial differences in the claims, there are certain areas of commonalty. There is a time-dependent magnetic or electric field produced, either from the motion of charged particle passing fixed magnets, or from an oscillating current in an electric coil wrapped around a pipe. The time-dependent magnetic or electric field yields a molecular disturbance which affects any particle with an electric charge. Most past theories were rejected by the scientific community because the observation was presented, often with little or no incorporation into the accepted theories of natural science. It is the intent of this paper to present a theory consistent with commonly accepted ideologies of science.
Proposed Theory-Macro Description
Although there are three different types of physical water treatment devices, we believe that the operating principles of the three devices are based on the same laws governing the physical and chemical behavior of water and scale-causing dissolved ions. The origin of scale problem is in a 'localized' supersaturation, and the physical water treatment eliminates the localized supersaturation, in which the scale-causing minerals such as calcium and magnesium ions are unstably hydrated or 'barely hanging in', thus ready to come out of the solution.
We propose that all physical water treatment devices provides the necessary energy such that the required overall free energy change, associated with the formation of a critical nucleus under heterogeneous condition, is achieved. Once the nucleus has reached a critical mass, the crystallization continues spontaneously until the precipitate is visible. This crystallization occurs within the water phase. Therefore the scale that is formed does not grow and encrust the pipe walls, but is suspended with the carrier fluid.
In addition to the change in nucleation site, the physical treatment also affects the crystal structure of the scale. Under treatment, the mineral ions are driven into creation of the non-adherent crystal form of the scale. This type of scale is often described as powdery and fluffy, and easily removed by turbulence and routine blowdowns of equipment.
As a result of the forced precipitation, the water becomes undersaturated and is then able to dissolve the scale that it comes in contact with. This explains the removal of scale deposits which has been formed prior to the physical treatment. Figure 4 shows a schematic diagram of the above-mentioned precipitation process for an induction cable technology.
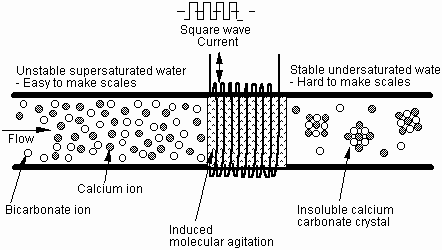
Fig. 4 Schematic diagram of precipitation process occurring in water treatment with induction technology
Permanent magnets produce molecular agitation when charged molecules or water molecules (i.e., polar molecule) enter the region under strong magnetic field. The molecular force experienced by the dissolved ions or water molecules is proportional to the product of flow velocity and the strength of magnetic field as
Molecular agitation in permanent magnet = V x B (1)
where V is the flow velocity and B is the strength of permanent magnet. Therefore, it is important to have a relatively large magnitude of flow velocity in the use of permanent magnet. The larger the flow velocity, the more efficiently the permanent magnet works. The frequency of molecular agitation comes from both the flow velocity and the number of permanent magnets. Hence, the optimization which should include flow velocity, pipe size, water hardness, etc. is extremely important in the use of a permanent magnet for the purpose of water treatment.
In the induction device, a cable is wrapped around a pipe. The cable is connected to an electronic unit that sends a complex, dynamic current to produce extremely small, time-varying magnetic fields inside the pipe. The time-varying magnetic field produces an induced, oscillating electric field inside the pipe, a phenomenon that is well known as the Faraday's law.
= - (2)
where E = induced electric field vector. The induced, oscillating electric field provides the necessary molecular agitation for scale prevention and removal. The major advantage of the induction device is in the non-invasive nature and its effectiveness does not depend on flow velocity. It does not require the cutting of a section of the pipe so that the installation is extremely simple. The drawback of the induction device is the fact that the treatment of water becomes weak at the center of the pipe where flow has the maximum velocity.
The device using an in-line electrode provides the water treatment where flow becomes maximized, which is one of the major strengths of this device. Furthermore, the effectiveness of this device does not depend on the flow velocity in pipe. However, this device requires a cutting of an existing pipe section.
Proposed Theory-Micro Description
To understand the mechanism of physical water treatment, we will begin with a discussion of the energy of nucleation. In order to understand the process of nucleation, which can be either heterogeneous or homogeneous, it is necessary to introduce the concept of Gibbs free energy of a substance. The Gibbs free energy of the formation of a substance is defined as the heat content for the formation of the substance minus the product of the temperature and the entropy. This function is often used to evaluate thermodynamic equilibrium. If the Gibbs energy is zero, the reaction is at equilibrium, while a spontaneous reaction will result in a reduction in the change in Gibbs free energy.
The Gibbs energy of nucleation is the summation of two distinct portions, a bulk energy term and a surface energy term.
DG(nucleation) = DG(bulk) + DG(surface) (3)
The bulk energy term can be defined as
DG(bulk) = -jKT [] = (4)
where j is the number of molecules in the nucleus, k is the Boltzmann constant, T is temperature, V is the molecular volume and a/ao is the ratio of the actual and equilibrium activities. This can be considered the ratio of supersaturation. Note that this term is always negative, indicating that this term always drives the reaction forward spontaneously. This is the energy released during crystallization from the making of bonds. The surface term can be defined as
DG(surface) = 4prg (5)
where r is the radius of the nucleus, and g is the interfacial energy. This term is the energy required to make the surface of the nucleus, and is positive in sign. In terms of radius, the Gibbs free energy can be thought of in the following manner.
DG(crystallization) = [function of radius] + [function of radius] (6)
At the initiation of nucleation, the number of molecules in the nucleus is small, making the bulk term relatively small. The surface term will dominate, making the overall Gibbs free energy positive in sign. Thus, the reaction will not occur spontaneously without energy input from outside the system. However, as the crystal grows, the bulk term will become more dominant and the reaction will eventually continue spontaneously. Figure 4 shows the qualitative trend of how DG (crystallization) varies with nucleus size for different supersaturation ratios.
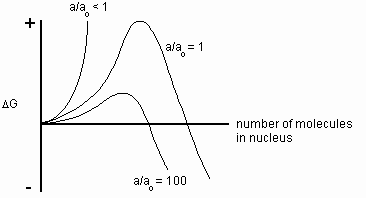
Fig. 4 Profiles of Gibbs free energy at three different supersaturation ratios
(i.e., a/ao <1, 1, and 100)
This figure shows how the Gibbs free energy of crystallization is affected by the size of the nucleus and the degree of supersaturation. Assuming the solution is supersaturated, the nucleus must grow beyond a critical size before the bulk term dominates and the reaction proceeds spontaneously. The energy that must be supplied into the system before this happens can be considered the activation energy of nucleation. In the vein of conventional reaction rate theory, the rate of nucleus formation can be expressed as
Rate of Nucleation = A exp [-G(activation)/kT] (7)
where A is similar to the frequency factor in reaction rate equation. This factor adjusts for the number of effective collisions as related to the total number of collisions. In this manner, it can be seen that the rate of nucleation is dependent on four basic quantities; the frequency factor, the temperature, the interfacial energy, and the degree of saturation.
It is well accepted that the nucleation that occurs in natural waters is predominantly from heterogeneous nucleation. Any foreign material which will reduce the interfacial energy between the solid and liquid phase will promote nucleation. Conventionally, this refers to an agreement in lattice types and energies, but can also occur when surface adsorption differs. This is the basis for the effect of the physical treatment of water.
The second proposed effect from the magnetic treatment concerns the force imparted by changing magnetic field. As the water experiences the changing magnetic field, the generated Lorentz force imparts force on all charged ions within the field. In the same manner that heat energy increases molecular vibration and stretches these bonds of hydration, the induced voltage from the changing magnetic field will similarly increase the energy of the system.
The forces imparted by the magnetic treatment are clearly smaller than the bond energies of solvation. Therefore, the magnetic treatment will not directly affect the macro-property of solubility. Rather, it is proposed that the energy from the magnetic treatment will cause an increase in the water-to-ion bond energy, resulting in a weaker attachment of the ions to the surrounding cluster of water molecules. In this scenario, the solvated ions are affected more by the large number of intermolecular collisions which occur naturally in the water flow. Referring back to equation 5, this indicates that the frequency factor (A) increases, resulting in a larger number of collisions successfully culminating in nucleation.
The Lorentz force imparted from the changing magnetic fields will affect the charged particles within its field. Again, the forces under discussion are not large enough to cause a shift in macro particles. However, it is adequate and sufficient for the Lorentz force to affect the dipole moment of the ions. It is conceivable that the force would induce a temporary dipole moment on a neutral molecule, but is more likely to shift the charge location on a polar molecule subtly. It is this concept which changes the morphology of the crystal formed.
When pure calcium carbonate precipitates naturally under typical environmental conditions, the predominant crystalline form can either be aragonite or calcite form depending on temperature or pressure. The difference in Gibbs free energy between the formation of calcite (-269.78 Kcal/mole) and aragonite (-269.53 Kcal/mole) is only -0.25 Kcal/ mole. It should be noted that there is no equilibrium condition for those two pure substances. The transfer or reaction is spontaneous as long as aragonite remains at specified temperature and pressure. For example, the pipe wall in a heat exchanger is more prone to form aragonite than calcite because of higher pipe wall temperature. In contrast, due to the physical treatment of water (using either electric or magnetic field) calcite will form in the liquid phase since the temperature is lower in the liquid phase.
If the standard dipole moments of the ions are disturbed by the magnetic treatment, the solvated ion will have a different energy with the evolving nucleus. Just as the heterogeneous nucleation rate increases due to lowered interfacial energy, a shift in dipole moment can also result in increased nucleation.
Discussion
Any theory of physical water treatment must be able to explain four distinct phenomena. The first is the immediate forced precipitation of calcium carbonate from water, the second is the predominant formation of the calcite (non-adherent) form of calcium carbonate, the third is the dissolution of calcium carbonate which had been formed prior to treatment and the fourth is the overall temporary nature of the treatment.
The forced precipitation is explained by heterogeneous nucleation theory. Dissolved ions are constantly participating in collisions with the impurities in the water phase. The small percentage of the collisions that are effective in nucleation are statistically accounted for by the frequency factor previously described. The induced voltage provided by the magnetic treatment changes the effectiveness of the collisions, increasing the number of collisions that result in nucleation.
The change in the frequency factor can be explained by the weakening of the hydrogen bond between the ion and the surrounding water molecules. The Lorentz force will orient the charges of the ions (both positive and negative) so that the surface charges of the ions which are colliding in the parallel direction to the electric field will be enhanced. Along with an increase in the kinetic energy of the colliding ions, the electric field will also increase the Coulombic attraction of the ions by increasing its dipole moment. All of these factors will improve the efficiency of the collisions, resulting in a larger number of resulting nuclei. This is the basis for the immediate precipitation that is observed from the physical treatment.
The explanation of how the physical treatment of water results in the formation of the non-adherent, crystalline form of calcium carbonate in the liquid phase is explained by the lattice energies of crystals. For untreated water, after a nucleus has been created, crystals in general will grow at the pipe wall in layers by forming the lattice structure which depends on temperature at the pipe wall. For calcium carbonate crystals at higher pipe wall temperature, this structure is the aragonite form, which is dendritic, dense, and adherent. In this structure, adjacent carbonate ions in each crystal layer are oriented in opposite directions as shown in Fig. 1. The Lorentz force produced by a water treatment device changes the random orientation of the carbonate ions in solution. As the carbonate ions come out of solution to form the next crystal layer, they are all oriented in the same direction due to this Lorentz force. When calcium carbonate crystallizes with this ordered and similar orientation of carbonate ions, the result is the formation of calcite and not aragonite. Therefore the observed change in adherent scale to non-adherent scale is explainable by a shift in crystal lattice structure.
The dissolution of scale which had been formed prior to physical treatment is explainable by the concepts of chemical equilibrium. Most natural waters are saturated or slightly less than saturated with calcium carbonate. What this means is that the following reaction is at equilibrium.
Ca+ HCO![]() CaCO (8)
CaCO (8)
Any change in concentration will shift the reaction based on LeChatelier's principle of equilibrium. Under physical treatment, additional calcium carbonate will be forced to precipitate in liquid phase, as calcite but not as aragonite. There will therefore be two reactions at equilibrium.
Ca+ HCO![]() CaCO (9)
CaCO (9)
Ca+ HCO![]() CaCO (10)
CaCO (10)
As the physical treatment increases the formation of water-born calcite, the concentration of bicarbonate ions will fall in Eq. (10). This depletes the reactants of Eq. (9) and will force this reaction to dissolve prior-formed aragonite to find a new level of equilibrium. The previously formed calcium carbonate solid in the form of aragonite (mostly localized at pipe walls) will thereby dissolve into solution, creating calcium and bicarbonate ions until a new state of chemical equilibrium is reached.
The last phenomenon is the documented temporary effects of physical treatment, which is strongly related to the above-mentioned removal of previous scale deposits. Once the water is treated and the calcite solid has formed, the system is not in chemical equilibrium. Referring again to Eq. (8), the reaction has been forced to the right, and there are not enough reactants to support the solubility constant. Therefore, some of the calcite solid will dissolve back into the solution until it reaches chemical equilibrium again. As the scale that is forced to precipitate and the previously deposited scale are redissolved, the water slowly reverts back into a state of equilibrium, explaining the temporary nature of the physical treatment. The solid that remains is in a stable state. The re-dissolving of aragonite back into solution occurs rapidly since it is a more stable form of calcium carbonate (?).
This paper has proved a standard scientific explanation for each of the reported phenomena associated with physical water treatment. These effects are well documented in literature, and the authors have directly observed the effects of physical treatment under strict controls. It is hoped that this discussion will help dispel the 'black magic' aura that has surrounded physical water treatment, and it can be studied and accepted as a legitimate treatment, rooted in science.
#3
The rate of nucleation of a solution or melt can be affected considerably by the presence of mere traces of impurities in the system. However an impurity that acts as a nucleation inhibitor in one case may not necessarily be effective in another; indeed it may act as an accelerator. No general rule applies and each case must be considered separately.
Many reported cases of spontaneous(homogeneous) nucleation are found on careful examination to have been induced in some way. Indeed, it is generally accepted that true homogeneous nucleation is not a common event.
The overall free energy change associated with the formation of a critical nucleus under heterogeneous conditions DG'crit, must be less than the corresponding free energy change, DGcrit, associated with homogeneous nucleation, i.e.
DG'crit = f DGcrit (1)
where the factor f is less than unity.
It has been indicated above that the interfacial tension, g, is one of the important factors controlling the nucleation process. Figure A shows an interfacial energy diagram for three phases in contact; in this case, however, the three phases are not the more familiar solid, liquid and gas, but two solids and a liquid. The three interfacial tensions are denoted by gcl (between the solid crystalline phase, c, and the liquid l). gsl (between another foreign solid surface, s, and the liquid) and gcs (between the solid crystalline phase and the foreign solid surface). Resolving these forces in a horizontal direction
gsl = gcs + gcl Cos q
or
Cos q = (gsl - gcs) / gcl (2)The angle
q, the angle of contrast between the crystalline deposit and the foreign solid surface, corresponds to the angle of wetting in liquid-solid systems.The factor
f in equation 1 can be expressed (Volmer, 1939) as f = [(2 + Cos q) (1 - Cos q)2] / 4 (3)Thus, when
q = 180o, Cos q = -1 and f = 1, equation 1 becomes DG'crit = DGcrit (4)When
q lies between 0 and 180o, f < 1; therefore DG'crit < DGcrit (5)When
q = 0, f = 0, and DG'crit = 0 (6)The three cases represented by equations 4-6 can be interpreted as follows. For the case of complete non-affinity between the crystalline solid and the foreign solid surface (corresponding to that of complete non-wetting in liquid-solid systems),
q =180o , and equation 4 applies, i.e. the overall free energy of nucleation is the same as that required for homogeneous or spontaneous nucleation. For the case of partial affinity (cf. the partial wetting of a solid with a liquid), 0<q<180o, and equation 7 applies, which indicates that nucleation is easier to achieve because the overall excess free energy required is less than that for homogeneous nucleation. For the case of complete affinity (cf. Complete wetting) q = 0, and the free energy of nucleation of zero. This case corresponds to the seeding of a supersaturated solution with crystals of the required crystalline product , i.e. no nuclei have to be formed in the solution. Figure B indicates the relationship between f and q.As mentioned above, the heterogeneous nucleation of a solution can occur by seeding from embryos retained in cavities, e.g. in foreign bodies or the walls of the retaining vessel, under conditions in which the embryo would normally be unstable on a flat surface. This problem has been analyzed by Turnbull (1950) for different types of cavity. The maximum diameter of a cylindrical cavity which will retain a stable embryo is given by
dmax = 4
gcl Cos q / DGv (7)where
DGv is the volume free energy for the phase transformation. If the system is heated, this reducing the supersaturation or supercooling and eliminating all embryos in cavities larger than dmax, and subsequently cooled, the embryos retained in the cavities smaller than dmax will grow to the mouth of the cavity. They will then act as nuclei only if the cavity size dmax >= 2rc, where rc is the size of a critical nucleus.__